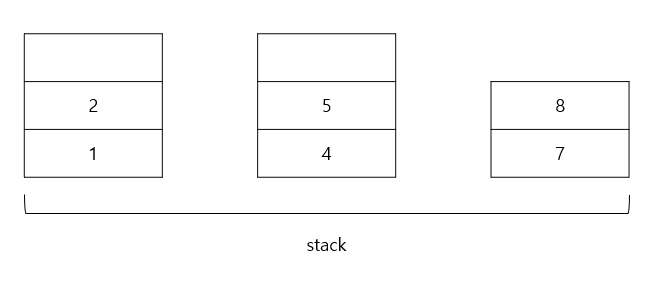
스택은 가장 나중에 들어온 자료가 가장 먼저 처리되는 LIFO(Last-In-First-Out) 자료구조이다. 구멍이 하나밖에 없는 병이라고 생각하면 이해하기 쉽다.
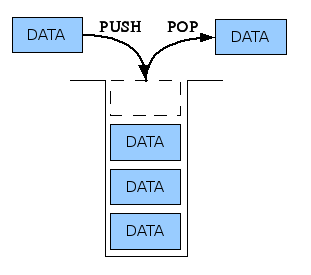
스택은 다음 4가지 operation을 지원해야 한다.
- pop() : 스택의 가장 위에 있는 데이터를 제거. (가장 최근에 추가된 데이터)
- push(item) : 데이터를 스택의 가장 위에 추가
- peek() : 스택의 가장 위에 있는 데이터를 리턴.
- isEmpty() : 스택이 비어 있을 때 True를 리턴.
3.1 Describe how you could use a single array to implement three stacks.
Approach 1: Fixed Division
리스트를 3등분한 다음 각각을 스택으로 활용하는 방법
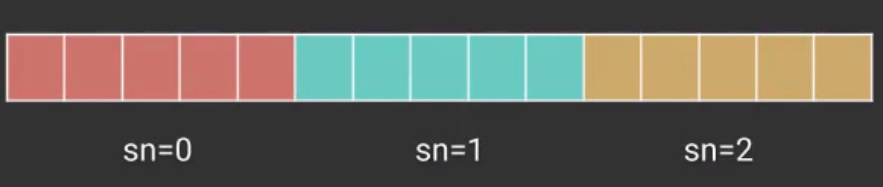
스택 사이즈를 동일하게 구성하고 각각의 스텍에 데이터를 넣는 방식이다.
간단하게 구현할 수 있지만, 스텍마다 입력한 데이터의 갯수가 다른 경우 비효율적으로 공간을 차지하게 된다.
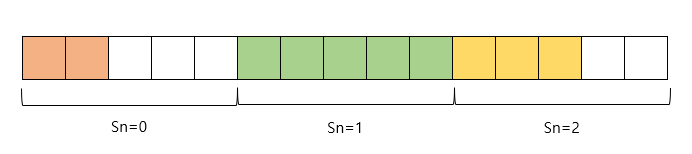
예를 들어 두번째 스텍은 데이터가 5개이고 나머지 스텍은 2개, 3개인 경우 어레이 안에 비어있는 공간이 생기게 된다. 이후 두번째 스텍에 데이터가 하나 더 들어오게 되면 어레이 안에 이미 빈 공간이 있음에도 전체 어레이를 늘려줘야 하는 비효율이 발생한다.
-
isEmpty(), isFull()

-
push
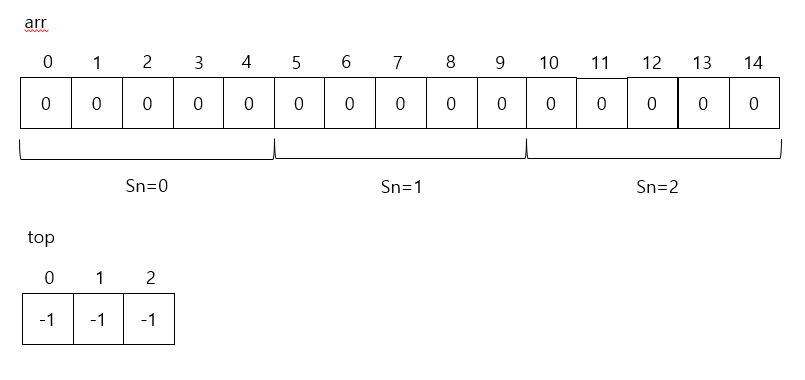
- push(10,0)
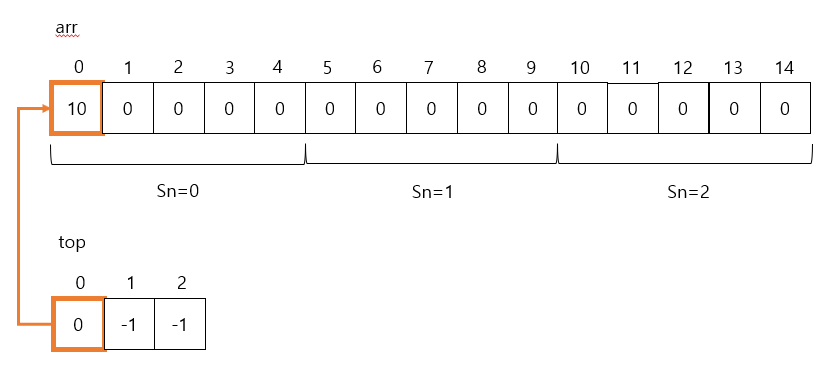
- push(20,0)
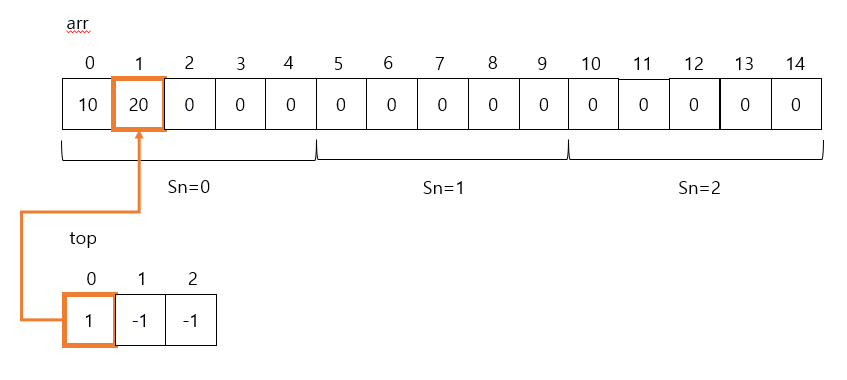
- push(11,1)
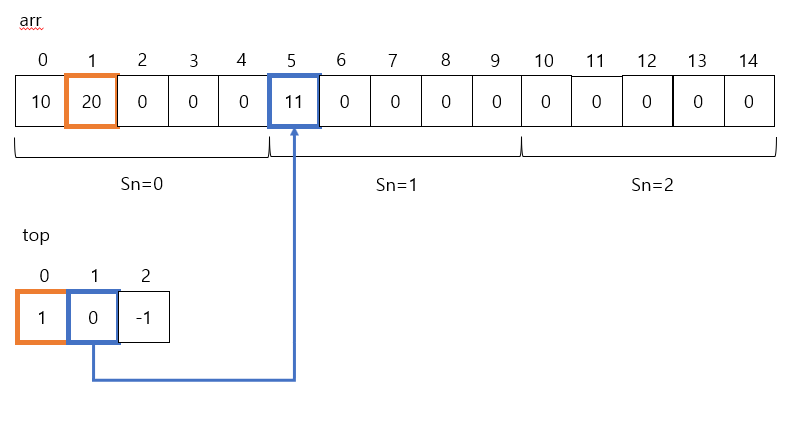
Approach 2: Flexible Divisions
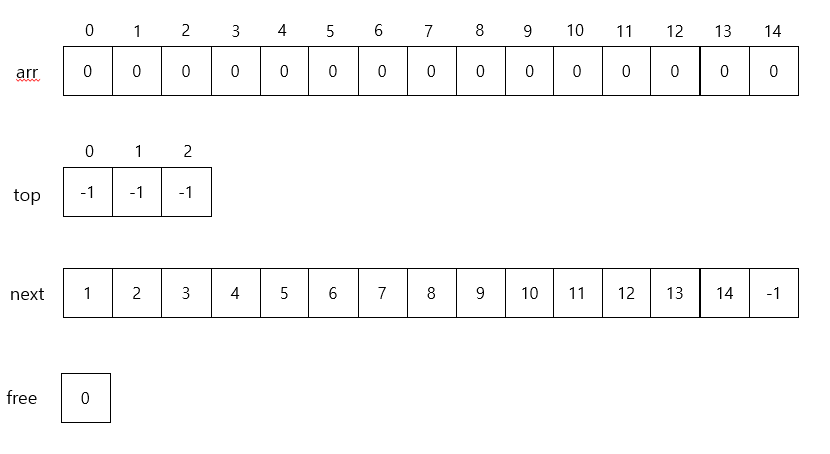
- push()
def push(self, item, stackNumber):
if self.isFull():
print("Stack Overflow")
return
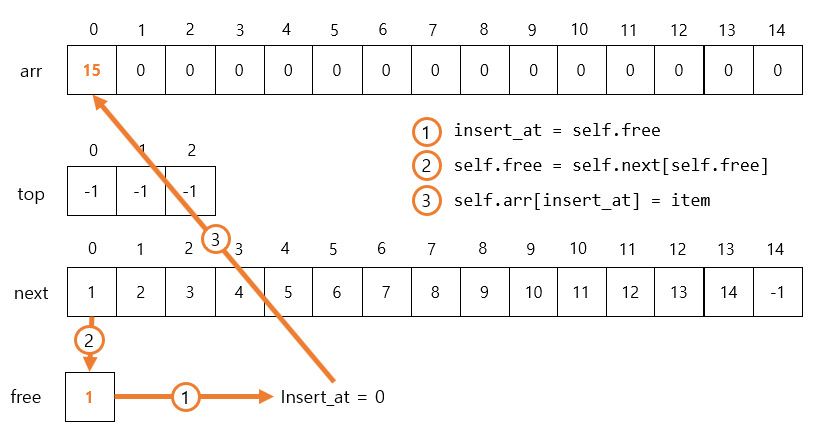
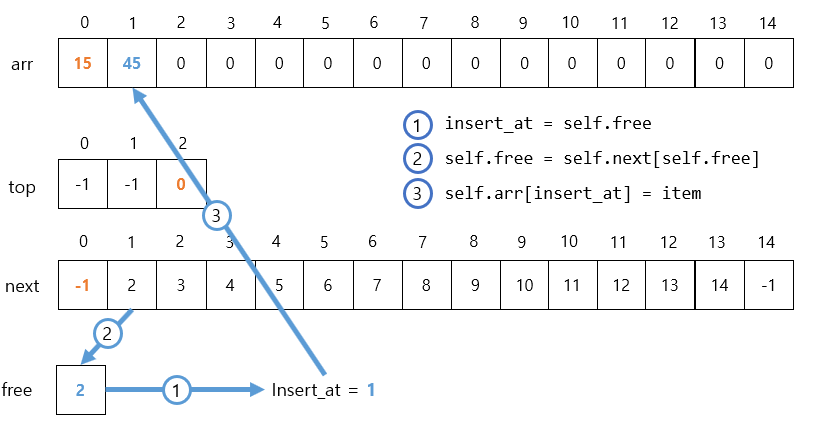
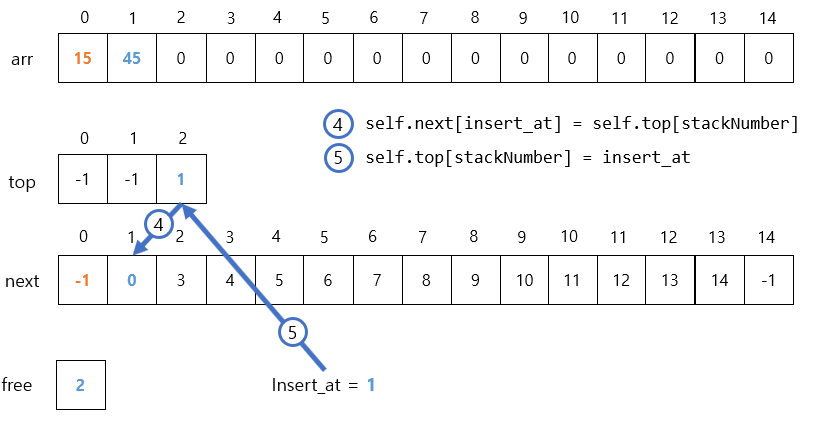
insert_at = self.free
self.free = self.next[self.free]
self.arr[insert_at] = item
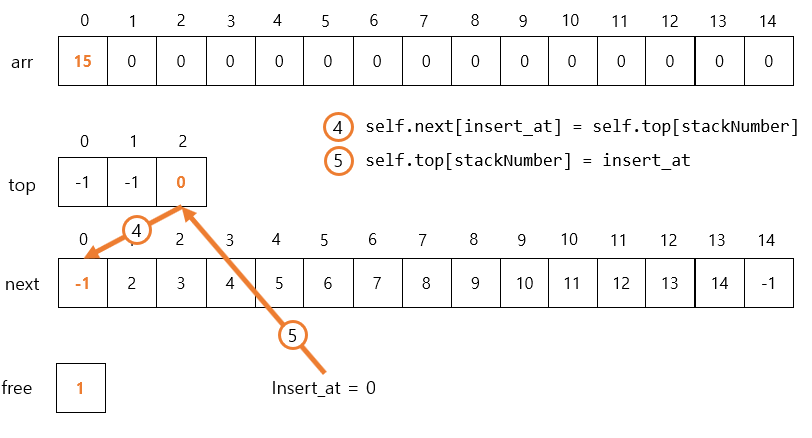
self.next[insert_at] = self.top[stackNumber]
self.top[stackNumber] = insert_at
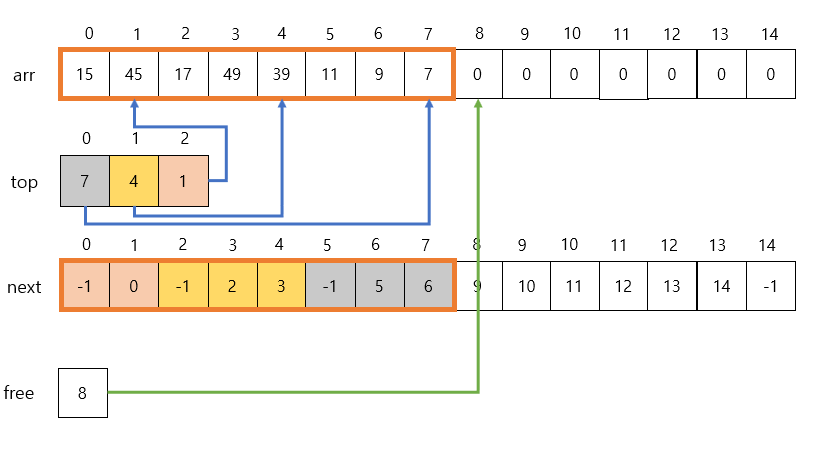
# Push some items onto stack number 2.
kstacks.push(15, 2)
kstacks.push(45, 2)
# Push some items onto stack number 1.
kstacks.push(17, 1)
kstacks.push(49, 1)
kstacks.push(39, 1)
# Push some items onto stack number 0.
kstacks.push(11, 0)
kstacks.push(9, 0)
kstacks.push(7, 0)
3.2 How would you design a stack which, in addition to push and pop, has a function min which returns the minimum element? Push, pop and min should all operate in 0(1) time.
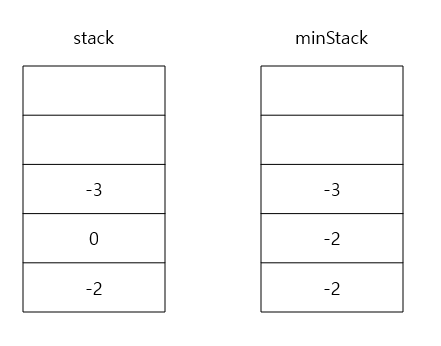
class Minstack:
def __init__(self):
self.stack = []
self.minStack = []
def push(self, val: int) -> None:
self.stack.append(val)
val = min(val, self.minStack[-1] if self.minStack else val)
self.minStack.append(val)
def pop(self) -> None:
self.stack.pop()
self.minStack.pop()
def top(self) -> int:
return self.stack[-1]
def getMin(self) -> int:
return self.minStack[-1]
3.3 Imagine a (literal) stack of plates. If the stack gets too high, it might topple. Therefore, in real life, we would likely start a new stack when the previous stack exceeds some threshold. Implement a data structure SetOfStacks that mimics this. SetOfStacks should be composed of several stacks and should create a new stack once the previous one exceeds capacity. SetOfStacks. push() and SetOfStacks. pop() should behave identically to a single stack (that is, pop () should return the same values as it would if there were just a single stack).
Stack of Plates ~ Cracking the Code (Python)
- capacity = 3, item이 8개인 경우
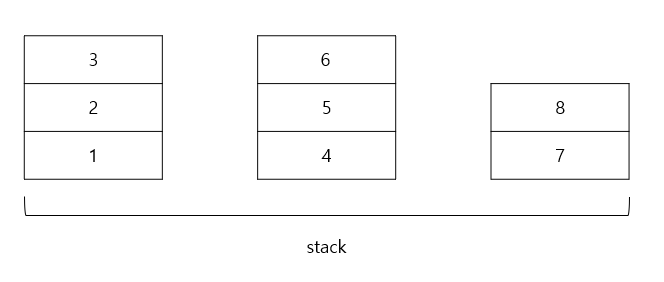
stacks = [[1,2,3],[4,5,6],[7,8]]
pop()
popAt(1)
popAt(0)
push(10)